Obim kruga i njegovih delova
Definicija kruga
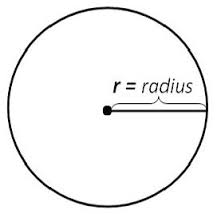
Krug je zatvoren skup tačaka ravni, čija je granica periferija kruga, odnosno kružnica. Matematika krug još odredjuje centrom (O) i poluprečnikom, odnosno radijusom koji obeležavamo sa (r) i to kao geometrijsko mesto tačaka ravni čija rastojanja od tačke O nisu veća od r, odnosno od poluprečnika kruga.
Krug se takodje može dobiti presekom ravno kroz loptu, odnosno njen centar.
Nekada se u matematičkoj terminologiji pod pojmom krug podrazumeva kružnica (kriva). U diferencijalnoj geometriji, krug krivine je isto što i oskulatorni krug, odnosno oskulatorna kružnica.
Definicija kruga po euklidskoj planimetriji: Krug je skup svih tačaka u ravni na jednakom rastojanju, koje se zovu poluprečnik ili radijus, od jedne tačke, koja se zove centar.
Krugovi su takodje i proste zatvorene krive, koje dele ravan na unutrašnjost i spoljašnjost. Ponekad se terminom krug označava unutrašnjost, a kružnica se onda naziva obimom. Obim je zapravo dužina kružnice.
Krug sa centrom u koordinatnom početku i poluprečnikom 1 se zove jedinični krug.
Svi krugovi su slični pa je posledica toga to što su obim kruga i njegov poluprečnik proporcionalni, kao što je to slučaj i sa njegovom površinom i kvadratom radijusa. Konstanta proporcionalnosti je 2π i π, redom, pa je tako površina kruga
Obim kruga
Obim kruga je zapravo vrednost dužine kružnice i on se dobija pomoću prečnika kruga, odnosno njegove prepolovljene vrednosti – poluprečnika koji se obeležava sa (r). Formula za izračunavanje obima kruga je 2πr, što znači da je obim kruga jednak dvostrukom proizvodu poluprečnika kruga i konstante π (pi) koja približno iznosi 3,14. Jednačina po kojoj je odnos obima i prečnika kruga jednak konstanti (pi) omogućava nam izračunavanje obima i površine kruga.
Sečenje kruga i obim njihovih delova
Linija koja seče krug u dve tačke je sekanta, a linija koja dodiruje krug u jednoj tački je tangenta. Tangentne linije su uvek pod pravim uglom sa poluprečnicima, (90 stepeni) segmentima koji spajaju centar sa tačkom na kružnici.
Deo sečice ograničen krugom zovemo tetivom, a najduža tetiva (ona koje prolazi kroz centar ) zove se prečnik ili dijametar i sačinjen je od dva poluprečnika. Površina dela kruga odsečenog tetivom se naziva kružni odsečak. Deo obima ograničen sa dva poluprečnika se zove luk, a površina u okviru tih poluprečnika i luka je kružni isečak. Odnos dužine luka i poluprečnika odredjuhe ugao između dva poluprečnika u radijanima.
Obim dela kruga koji je ograničen sa dva radijusa i kružnim lukom izračunavamo uz pomoć ugla izmedju dva poluprečnika. Ako je na primer ugao 60 stepeni, a ukupan zbir stepena u krugu je 360 stepeni, jasno je da da je reč o šestini dužine luka kružnice. Tako će obim ovog dela kruga biti jednak dužini dva poluprečnika i dužini jedne šetine ukupnog obima kruga. O = 2r + 1/6 x ( 2 π r).