Površina i zapremina lopte i njenih delova

Lopta je geometrijsko telo koje je ograničeno sferom.

Jedna od definicija lopte je da je to skup tačaka koje se nalaze na jednakoj ili manjoj udaljenosti dužine (r), od zadate tačke (0). Najvažnijie veličine jedne lopte su njena površina i zapremina lopte.

Obično se centar lopte obeležava sa (0) a poluprečnik lopte sa (r).

Definicije isečaka lopte

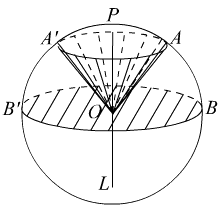
Loptin isečak je geometrijsko telo koje se dobija obrtanjem kružnog isečka oko dijametra (prečnika) a koji nema unutrašnjih tačaka sa lukom isečka kruga.

Postoji loptin isečak prve vrste i loptin isečak druge vrste.

U slučaju kada je poluprečnik kružnog isečka na obrtnoj osi, odnosno na dijametru, reč je o isečku prve vrste.

Ako dijametar pak ne seče luk kružnog isečka, onda je reč o isečku lopte druge vrste.

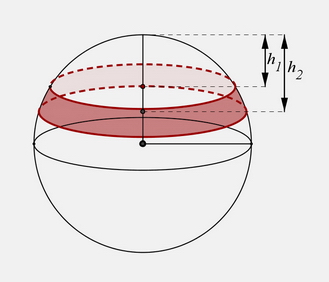
Loptin pojas

Loptin pojas takodje može biti prve i druge vrste. Pojas koji je ispupčen odnosno konveksan je pojas prve vrste a ako je konkavan – udubljen, reč je o pojasu druge vrste.

Pojas jedne lopte je zapravo deo loptine sferne površi, koji se nalazi izmedju dve paralelne presečene ravni.

Loptin pojas se u matematici naziva još i zona.

Postoji i loptin segment. To je deo lopte izmedju dve presečene ravni i jedne od dve njene sferne površi. Sloj lopte je njen deo koji se nalazi izmedju paralelnih presečenih ravni.

Svaki presek lopte je ravni krug.

Formula za površinu lopte

Površina lopte se računa prema formuli: S = 4πr²

Površina lopte jednaka je proizvodu kvadrata poluprečnika lopte, konstanti  π (3,14) i broja 4.

Obrazac za izračunavanje zapremine lopte

Formula za računanje zapremine lopte je

V = 4/3 π r³

Zapremina lopte jednaka je proizvodu tri četvrtine, konstante π (3,14) i poluprečniku na trećen stepenu (na kub).

Zapremina odsečka lopte

Ako je r – poluprečnik lopte a h visina odsečka, onda je zapremina odsečka  V = πh² /3 x (3r-h)

Zapremina loptinog sloja

V = πh / 6 x (3r1² x 3r2² + h²)

Izvodjenje formula preko integrale