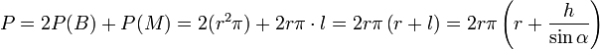Površina i zapremina valjka

Valjak ili cilindar (ime potiče od od grčke reči kýlindros, što znači kotrljati, valjati) je konveksno geometrijsko telo. Moguće jedefinisati valjak uz pomoć jedne elipse i duži u prostoru.

Ako  se jedno teme date duži postavi u centar odredjene elipse, a elipsa neprekidno umnožava duž nje, dobijamo valjak. Takodje, radijusi ove elipse su ujedno radijusi valjka, dužina odredjene duži je takodje dužina izvodnice valjka, a rastojanje između ravni kojima pripadaju dve najudaljenije elipse je u ovom slučaju visina valjka.

Prava kojoj pripada odredjena duž se zove osa valjka, a elipsa od koje je razvoj tela počeo, zove se baza valjka.

Površ koja ograničava valjak, u slučaju da se valjku oduzmu dve elipse sa centrima u temenima odredjene duži, se naziva omotačem valjka.

Vrste valjaka

U slučaju da je osa valjka normalna na bazu valjka, ovo telo se naziva pravi valjak, i kod njega su dužine izvodnice i visine podjednake. U suprotnom slučaju, reč je o kosom valjku, i njegova izvodnica je uvek duža od visine. U zavisnosti od toga da li je baza prava elipsa ili krug, valjak još može biti eliptični, odnosno kružni. Kao i svako geometrijsko telo, valjak ima svoju površinu i zapreminu.

Površina valjka

Površina kružnog jednakostraničnog valjka (P) je odredjena  kao zbir površine omotača valjka i dupla površina njegove baze. Površina omotača se računa kao proizvod dužina obima baze i izvodnice valjka. Formula za izračunavanje površine valjka je sledeća:

Objašnenje za obrazac– P(B) predstavlja površinu baze, a P(M) površinu omotača valjka. Površina omotača je već opisana kao:

Potrebno je voditi računa da kod pravog valjka važi pravilo da je h=l. Kod kosog valjka izvodnica ne mora uvek biti data eksplicitno. Možemo je izračuati uz omoć dužine visine (h) i jednog ugla. To je obično ugao između baze i ose valjka, ili njegov komplement, odnosno ugao između normale na bazu i ose valjka. Tako se mogu dobiti dve naredne formule:

           

Zapremina valjka

Zapremina valjka (V) se dobija kao proizvod površine bazne elipse i visine valjka. Njena formula bi tako bila sledeća:

Ovde B predstavlja površinu baze, a h visinu valjka. I ovde važi da, ako visina valjka nije data eksplicitno, ona se može odrediti pomoću dužine izvodnice i jednog ugla, kao što je to opisano u pretodnom primeru.

Ostale izvedene formule

Oznake su: r je poluprečnik kružne baze, h je visina valjka, l je dužina izvodnice i α za ugao između baze i ose valjka.

Formula za pravi kružni valjak:

Formula kosi kružni valjak:

Formule dobijene pomoću osnog preseka i poprečnog preseka

U ovim slučajevima mogu se dobiti kombinovane formule jer poznavajući dužine odnosno vrednosti na primer poluprečnika  preseka kod pravog valjka, možemo dalje izračunati obim baze, pa tako i površinu baze i omota.U ovom slučaju nam mora biti poznata visina valjka kako bismo iztačunali površinu ili zapreminu. Kada je osni presek u pitanju, ovde će nam biti lako da dobijemo vrednosti dužine visine i površine omotača valjka, kao i baze jer će u tom slučaju poluprečnik baze jednak polovini dužine isnovice osnog preseka.