Kako se izračunava površina trapeza
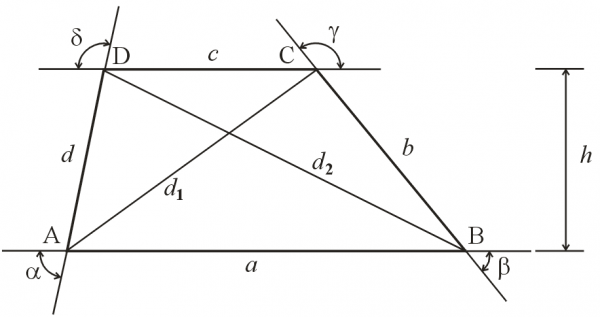
Trapez je konveksni četvorougao, sa dve paralelne naspramne stranice. Jedna od dve stranice koje su paralelne naziva se baza trapeza a druge dve koje nisu paralelne zovu se kraci trapeza.
Važni elementi trapeza su i dve dijagonale koje se uvek seku.
Rastojanje izmedju dve paralelne stranice je visina trapeza i obično se obeležava sa h u geometriji.
Zbir uglova na jednom od krakova je 180°, odnosno α + δ = β + γ = 180°.
Vrste trapeza
Matematika i trigonometrija poznaju nekoliko vrsta trapeza:
Jednakokraki trapez, koji ima jednake krake i jednake uglove na osnovici.
Pravougli trapez kod koga je jedan krak pod pravim uglom u odnosu na bazu
Paralelogram – kod koga je i drugi par stranica, odnosno krakova medjusobno paralelan.
Romb, koji nije paralelogram ali ima sve medjusobno jednake stranice
Pravougaonik koji jeste paralelogram ali su mu stranice normalne jedna na drugu, odnosno pod uglom od 90 stepeni.
Kvadrat koji ima sve jednake stranice, pod pravim uglom, odnosno stranice koje su normalne jedna na drugu.
Osnovice trapeza su paralelne linije. Visina trapeza koja je povučena iz krajeva manje osnovice pravi sa većom osnovicom prav ugao i razlikuje na trapezu odsečke. Visina, odsečak i odgovarajući krak trapeza tako prave jedan pravougli trougao. Osnovice obično obeležavamo sa a i b, krake trapeza sa s i d, a odsečke sa x i y.
Kod jednakokrakog trapeza kraci su jednaki (c=d), kao i odsečci na većoj osnovici trapeza (x = y).
Kod pravouglog trapeza jedan krak je jednak visini trapeza, a odsečak x je jednak razlici veće i manje osnovice trapeza.
Tangentnii trapez je trapez kome možemo upisati kružnicu. Kod ovog trapeza zbir suprotnih stranica je jednak ( a + c = b + d ).
Površina trapeza i izračunavanje
Površina trapeza je veličina njegove unutrašnjosti, a izražava se u mernim jedinicama: kvadratni metar (m2), kvadratni decimetar (dm2), kvadratni centimetar (cm2) itd.
Površina trapeza izračunata preko srednje linije iznosi: P=m×h, gde je m- srednja linija (srednjica, koja je paralelna s osnovicama), koja se računa prema formuli (a+b)/2, a h je visina.
Površinu trapeza možemo računati i preko dijagonale. Površina pomoću dijagonale se može dobiti ako se dijagonale seku pod pravim uglom. U tom slučaju se primenjuje teorema koja glasi: Površina četvorougla s normalnim dijagonalama jednaka je polovini proizvoda dužina njegovih dijagonala.
Površina nepravilnog trapeza
U slučaju nepravilnog trapeza, njegova površina se može razdvojiti na kvadrat ili pravougaonik i na dva trougla. Konačna površina se dobija sabiranjem dobijenih površina.