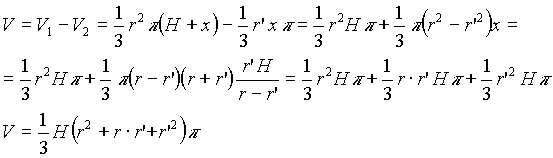Površina i zapremina kupe
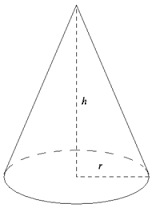
Kupa ili konus je geometrijsko telo koje matematika obično definiše kao geometrijsko mesto tačaka koje čine sve duži izmedju elipse koja je smeštena u jednoj ravni i tačke koja se nalazi van te ravni. Elipsa se naziva još i baza kupe a tačka je teme kupe.
Prava koja prolazi kroz centar baze i teme kupe, naziva se osa kupe. Ako je ona prava i normalna na kupinu bazu, reč je o pravoj kupi. U suprotnom slučaju, kupa će biti kosa.
Rastojanje izmedju temena kupe i projekcije temena na ravan baze kupe je visina kupe.
Bilo koja duž koja će spojiti teme sa nekom od ivičnih tačaka baze kupe je njena izvodnica.
Prava kupa ima sve jednake izvodnice, odnosno iste dužine. Kosa kupa ima najviše dve izvodnice koje imaju jednaku dužinu.
Obrazac za izračunavanje površine kupe
Površina kupe je zbir površina njenog omotača i baze kupe. Omotač kupe je zapravo skup svih duži koje spajaju ivicu osnovice kupe sa njenim temenom. Ako je baza kupe krug, ivica je onda kružnica.
Ako bismo razmotali odnosno razvili omotač jedne kupe, videli bismo da ćemo dobiti zapravo kružni isečak. Poluprečnik ovog isečka je u tom slučaju je izvodnica kupe (s). Ugao koji je pokriven se u tom slučaju prema punom krugu odnosi kao obim baze kupe prema obimu kruga čiji je poluprečnik (s).
Površina baze kupe je zapravo površina kruga sa poluprečnikom (r) što iznosi Pb = r²π. Zbir ovedve vrednosti daće nam površinu kupe.
Tako formula za površinu prave kupe izgleda ovako:
Zapremina kupe
Zapremina kupe jednaka je trećini proizvoda površine njene baze sa rastojanjem temena od ravni u kome se nalazi baza, a ovo rastojanje se naziva visina kupe. Zapremina kose kupe računa se na isti način.
Formula za zapreminu kupe tako je:
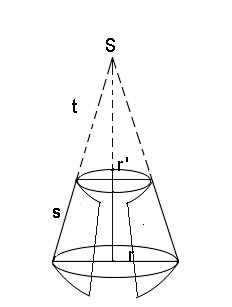
Površina i zapremina zarubljene, krnje, kose ili zaobljene kupe računa se na drugačiji način.
U slučaju zarubljene kupe, najpre izračunamo zapreminu kupe kao danije zarubljena ili krnja, a onda oduzmemo zapreminu koja nedostaje.
Zarubljena kupa nastaje rotacijom jednakokrakog trapeza oko njegove ose simetrije ili presecanjem prave kupe ravni paralelnoj osnovi kupe.
Formula za površinu zarubljene kupe:
Formula za zapreminu zarubljene kupe: