Površina i opseg romba
Izračunavanje površine i opsega romba
Romb je u geometriji četvorougao iz grupe paralelograma koji imaju sve stranice jednakih dužina.Karakteriše ga proizvoljna veličina ugla izmedju njegove dve strane i koja može da varira.
Poseban slučaj je romb koji ima stranice normalne jedna na drugu i takav romb matematika poznaje zapravo kao kvadrat.
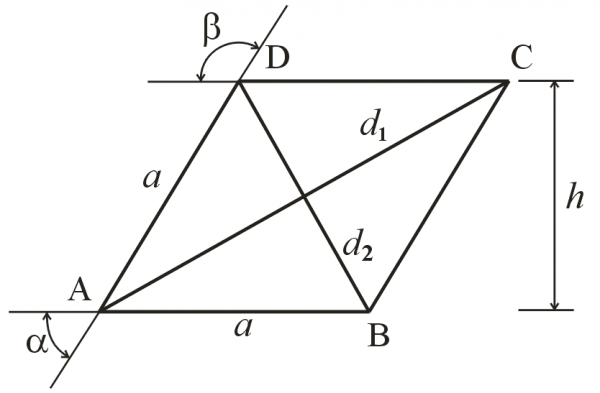
Iz pravila jednakosti strana, sledi da su naspramni uglovi romba jednaki, a to znači da postoje samo dve različite veličine uglova koje prave strane romba a koje obeležavamo sa : α i β – (alfa i beta).
Takodje, pravilo o zbiru uglova u četvorouglu jednoznačno odredjuje vrednost veličine drugog ugla, u slučaju da nam je jedan od uglova poznat. To znači da je romb definisan samo dužinom stranice i jednim uglom. Opseg ili obim romba jednak je zbiru vrednosti njegove 4 strane: O = 4a.
Dijagonale romba
Pravilo je da su uglovi izmedju dijagonala romba koje se seku u njegovom centru pravi, odnosno da imaju 90 stepeni.
Površina romba se može tako računati preko dijagonala: Ako su dijagonale romba d1 i d2, onda je obrazac za izračunavanje površine: P= d1 * d2 / 2
Stranice romba
Površina romba se može izračunati i preko stranica. Pošto je romb ujedno i paralelogram, njegovu površinu možemo računati i kao površinu paralelograma. U tom slučaju, površina romba jednaka je dvema površinama jednakostraničnih trouglova stranice. Podsećamo da polovine dijagonala romba i stranica romba obrazuju pravougli trougao.
Kako izračunati površinu romba na drugi način? Površina romba može da se izračuna i uz pomoć vrednosti njegove visine (h). Visina je u ovom slučaju i visina jednog od dva trougla koji čine romb. Formula za ovakvo računanje je: P = a * h, gde je a – dužina stranice romba.
Pitagorina teorema i romb
Pitagorina teorema koja važi za pravougli trougao, našla je svoju primenu i kod romba s obzirom na to da se isti sastoji od trouglova. Teorema glasi: Kvadrat nad hipotenuzom jednak je zbiru kvadrata nad katetama pravouglog trougla. U situaciji kada ne poznajemo dužinu stranice romba, možemo ih izračunati uz ovu teoremu, ako nam je na primer poznata dužina dijagonala romba. Tako će kvadrat stranice romba biti izračunat prema sledećoj formuli: a2 = (d1/2)2 + (d2 /2) gde je a – osnovica romba, d1 – duža dijagonala romba a d2 – kraća dijagonala romba.