Površina kvadra i kocke

Površina kvadra

Jedna od definicija koju matematika nudi objašnjavajući kvadar glasi: Kvadar je geometrijsko telo koje je omedjeno sa 6 medjusobno normalnih pravougaonih površi.

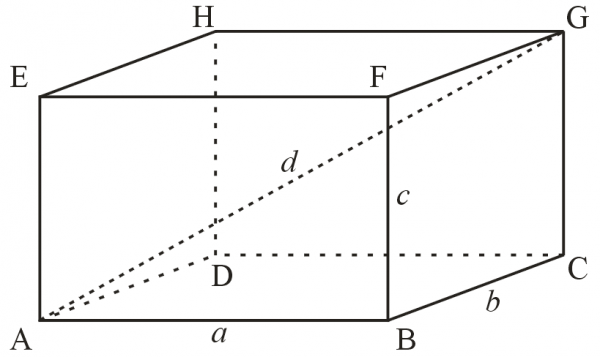
Ove površi se dele na tri para medjusobno naspramnih, paralelnih, jednakih površi a koje se mogu odrediti sa tri dužine a, b и c (c se nekada obeležava sa –h- odnosno visina kvadra). Ove tri dužine se tim redom nazivaju širina, dužina i visina kvadra.

Poseban slučaj je kvadar koji ima sve jednake ivice i u tom slučaju je reč o kocki.

Postoji sfera maksimalnog poluprečnika koja može da stane u kvadar, ali ona nije upisana u kvadar zato što ne dodiruje sve njegove površi. Poluprečnik ove sfere jednak je polovini dužine najkraće ivice kvadra.

Sfera može biti upisana u slučaju da su sve ivice kvadra jednake, odnosno kada je u pitanju kocka.

Formula za izračunavanje površine kvadra je P =  2 x (ab x ac x bc), odnosno, površina kvadra je jednaka zbiru površina pravougaonika koji ga čine.

Zapremina kvadra računa se kao proizvod dužina njegove tri strane V =  a x b x  c

Velika dijagonala kvadra jednaka je kvadratnom korenu iz zbira kvadrata svih stranica.

Površina kocke

Kocka  (grč. Hexáedron)  je telo sa šest površina  koje se još naziva i heksaedar. Kocka je jedan od 5 pravilnih poliedara. Omedjena je sa 6 kvadratnih površi koje su spojene tako da čine telo koje ima 12 duži i osam temena.

Kocku možemo definisati i kao poseban slučaj kvadra koji ima sve jednake stranice.

Kocka se u prostoru može definisati pomoću jedne tačke iz Rn, dužine ivice kocke, kao i sa n vektora koji čine pozitivno orjentisanu ortonormiranu bazu Rn.

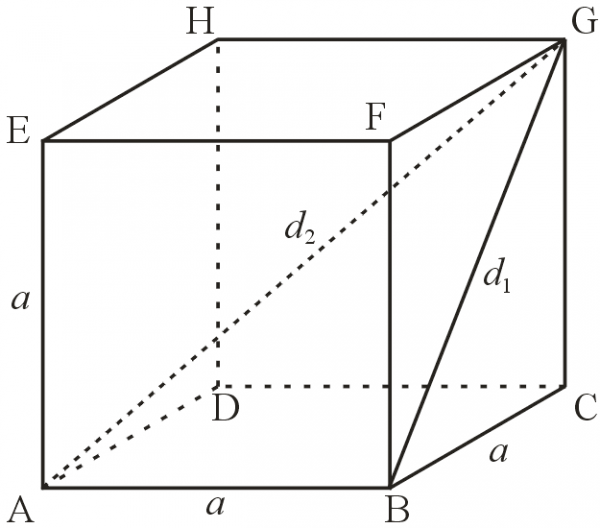
Mala dijagonala kocke jednaka je proizvodu kvadratnog korena broja 2 i vrednosti dužine stranice kocke (a). Ovo Pitagorino pravilo možemo koristiti u izračunavanju površine kocke preko dijagonala, u slučaju da su nam one poznate a stranice kocke nepoznate. Pošto je mala dijagonala (a x 1,41), stranicu ćemo dobiti tako što dužinu male dijagonale podelimo sa korenom iz broja 2 odnosno sa 1,41. Kada smo dobili stranicu kocke, površinu dobijamo po formuli P = 6a²Velika dijagonala kocke jednaka je proizvodu kvadratnog korena broja 3 i vrednosti dužine stranice kocke.

Radijus upisane kružnice je a /2

Analogija kocke u četriri dimenzije zove se hiperkocka. Ona se sastoji od osam jednakih kocaka.

Obrazac za površinu kocke je P = 6a², što znači da je površina kocke kednaka zbiru površine 6 kvadrata od kojih se sastoji. Kocka je i četvorostrana prizma i  spada u paralelepipede pa je njena mreža  sastavljena  od 6 jednakih kvadrata.